There seems little point in posing a maths question if the intention is to trip someone up, especially if you create doubt over whether a right answer is possible.
I had previously seen the following example spread widely in 2019, and it has reappeared many times since: 8 ÷ 2(2x2) = ?
But this one has also appeared: 5 + 6 x 4 = ?
There is one very clear reason why the answer to the first question is 1, but this same reason is why the answer to the second could be either 44 or 29.
BODMAS has been taught in British schools since the 1920s, prescribing how you should solve maths problems: Brackets, Orders, Divide, Multiply, Addition, Subtraction. Known as PEDMAS in the United States because of the alternative use of parentheses and exponents as mathematical terms, these abbreviations were created in the hope of becoming acronyms ingrained in the heads of schoolchildren – I think they eventually got there.
When I originally saw 8 ÷ 2(2x2), I knew the answer could only be 1, because brackets were used: 8 ÷ 2(2x2) = 8 ÷ 2(4) = 8 ÷ 8 = 1.
However, 5 + 6 x 4 could be answered linearly or using BODMAS, creating two different answers:
Linear: 5 + 6 x 4 = 11 x 4 = 44
BODMAS: 5 + 6 x 4 = 5 + 24 = 29
This is usually the end of it, but I realised it was never really explained at school why this rule even exists, and it is down to how much each mathematical operator changes the eventual answer. Multiplication and division are simply adding or subtracting one number many times, so it would make sense to act upon those first, but you should always simplify by answering brackets first – writing 5 + 6 x 4 as 5 + (6 x 4) also makes clearer what is meant to be happening.
 |
| Left to right: Casio SL-310UC, Canon LC-83M, HP 35s |
However, while BODMAS confirms that multiplication should be done before addition, dividing does not need to be done before multiplying, or subtraction before addition, so trying to create an acronym creates a misnomer as well. Calculators that implement BODMAS are programmed to multiply or divide, whichever comes first in the equation, followed by adding or subtracting, again whichever comes first.
But you can even get a different answer based on the calculator you use. I tried this with a Casio SL-310UC, a basic calculator, and the answer produced was 44, because it calculated each segment of the question as you go: pressing the multiply button after entering 6 produced the answer “11” on screen, before entering 4 and pressing the equals button.
Meanwhile, the Canon LC-83M, a 1980s slide rule calculator, only produces an answer when you press the equals button, down to the “Algebraic Operating System” displayed on the case. BODMAS is built into the calculator, guaranteeing the answer of 29 in this case.
To make things extra complicated, the HP 35s, a sophisticated programming scientific calculator, can produce both answers. In Reverse Polish Notation, you enter your numbers first, then enter what you want to do with them, building numbers in a stack – this relies upon the user to remember BODMAS to multiply the 6 and 4 first, instead of starting with the 5 and adding the 6. Changing the HP 35s to the standard Algebraic function used by the other two calculators, BODMAS now automatically applies, producing the answer 29.
With calculators now mostly bought for use in schools, adherence to BODMAS is expected, along with the ability to enter equations exactly as they appear on the page. Knowing what you are entering is more important than knowing how the calculator processes it – most instruction manuals therefore add a disclaimer confirming the manufacturer does not take responsibility for any answer generated.

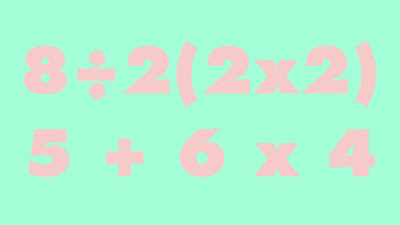
No comments:
Post a Comment